[기계학습] 뉴턴-랩슨법 Newton's Method

 

 

뉴턴랩슨법  Newton's Method 이란?

뉴턴랩슨법  Newton's Method 은 해를 구하는 방법 중 하나로, 불필요한 경우를 제외한 숫자를 대입해서 효율적으로 해를 찾아주는 방법이다

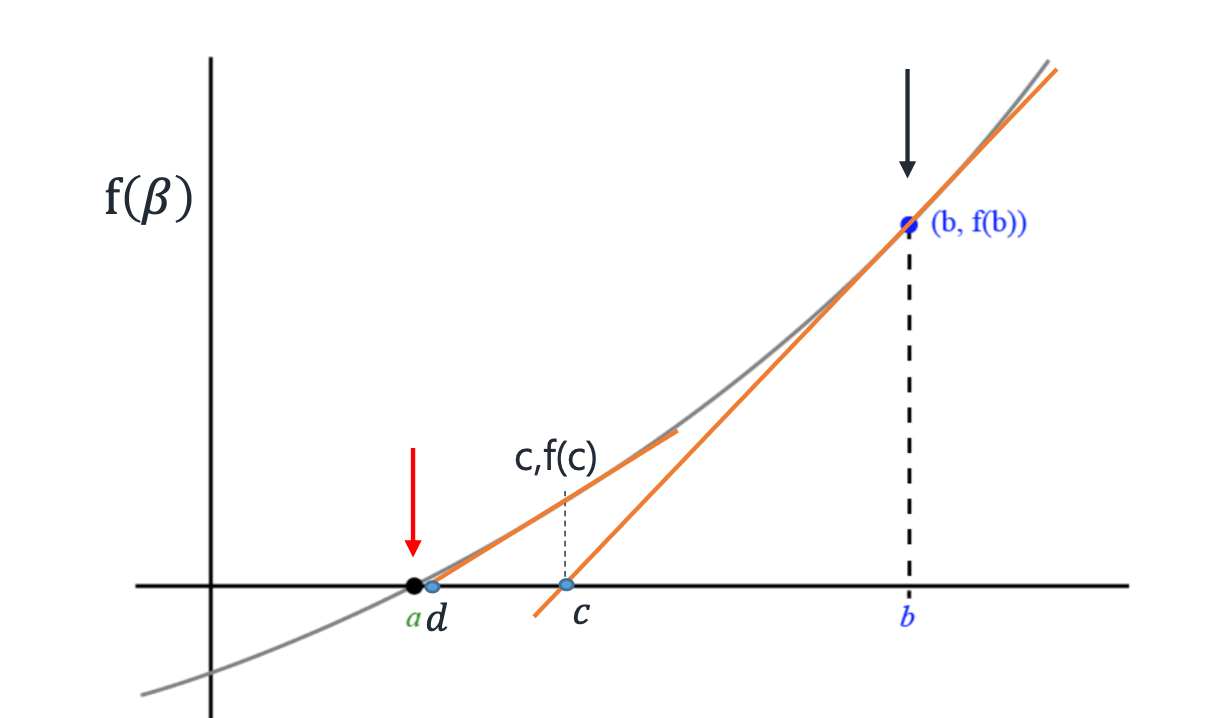
위 그래프에서 함수값이 0되는 지점 a를 찾거나, 혹은 a 와 가깝게라도 함숫값이 0에 가까워지는 지점을 찾아야하는데, 뉴턴 랩슨법을 통해 빠르게 찾을 수 있다

그럼 뉴턴랩슨법으로 어떻게 찾을 수 있을까 !!!!

바로 접선을 이용하면 된다

위 그래프처럼 β=b 지점에서 시작한다고 해보자. b 지점에서 접선을 구하면 β축과 만나는 점 c를 구할 수 있다
그래프에서 볼 수 있듯이 점 c 가 b 보다 우리가 구해야하는 a 에 더 가까운 것을 알 수 있다
그럼 이제 c 가 다음의 β값이 되는 것이다. 그리고 점 c 에서 같은 방법으로 접선과 β축과 만나는 점 d 를 구한다
이렇게 반복하다보면 함수값을 0으로 하는 점과 가깝게 β 를 찾을 수 있다

이런 방식으로 해를 구하는 것을 뉴턴 랩슨법이라고 한다

일반화

이제 일반화를 해보자

 

처음에 넣는 값을 b, 함수 f(β)에 b를 넣은 값을 f(b)라고 한다. 그럼 b에서 접선의 기울기는 f′(b) 이다.
그리고 다음에 넣을 값을 c 라고 하자. 

위 챕터에서 본 함수의 상황에 대입해보면 위 그래프와 같고, 이것을 수식으로 표현아면 아래 식과 같다

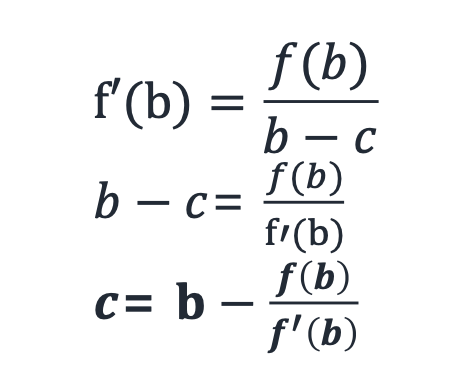
이렇게 다음에 넣을 값을 찾을 수 있으므로 이 과정을 함수값이 0에 가까이갈때까지 반복하면 된다

 

뉴턴랩슨법을 이용하여 Likelihood function 최대화 하기

Likelihood 를 최대화한다는 것은, 최대화시키는 지점인 β일때 미분값이 0 이 되어야한다

이 점을 참고하여 뉴턴랩슨법을 아래와 같이 적용할 수 있다

** Hessian Matrix 란?

함수를 2번 미분하여 Gradient 변화량을 구해 Gradient가 0인 지점을 찾아내는 것이다
또한 이를 통해 그래프가 아래로 convex 한지 위로 concave 한지도 알 수 있다

아래 과정을 통해 더 자세히 살펴보자

가정

1. 데이터 집합 X와 이진 분류를 위한 로지스틱 회귀 모델 사용.
2. 로지스틱 회귀 모델의 파라미터를 β로 나타냄.
3. 최대 우도 추정을 통해 로지스틱 회귀 모델의 파라미터 β를 찾으려고 함.

단계

1. 초기 추정치 설정: 최대 우도 추정을 시작하기 위해 초기 파라미터 추정치 β0를 설정한다.

2. 로그-가능도 함수(Log-Likelihood) 계산: 주어진 데이터 집합 X에 대한 로그-가능도 함수(log-likelihood)를 계산한다. 로그-가능도 함수는 보통 로지스틱 회귀에서 로그-우도 함수로 나타난다. 이것을 l(β)로 표시한다.

3. Gradient 계산: 로그-가능도 함수 l(β)를 β에 대해 미분하여 Gradient를 계산한다. 이것은 로그-우도 함수의 첫 번째 도함수이다.

4. Hessian Matrix 계산: 로그-가능도 함수 l(β)를 미분하여 Hessian Matrix를 계산한다. 이것은 로그-우도 함수의 두 번째 도함수로, β에 대한 미분의 미분이다.

5. 파라미터 업데이트: 뉴턴-랩슨 방법을 사용하여 파라미터를 업데이트한다. 

6. 수렴 확인: 일정 조건을 충족할 때까지 반복적으로 위의 단계를 수행한다. 일반적으로 뉴턴-랩슨 방법은 최적화 문제에 빠르게 수렴하므로, 일정 반복 횟수 또는 수렴 기준을 설정하고 해당 기준을 충족할 때까지 반복한다.

7. 최적 파라미터 추정치: 뉴턴-랩슨 방법을 통해 최적의 파라미터 추정치 β를 얻게 된다. 이 추정치는 주어진 데이터에 대해 가능도를 최대화하는 모델의 파라미터이다.

이렇게 뉴턴-랩슨 방법을 사용하여 가능도를 최대화하는 것은 로지스틱 회귀와 같은 최적화 문제에서 유용한 기법 중 하나이다. 
Hessian Matrix를 사용하여 더 빠른 수렴을 제공하며, MLE를 효과적으로 수행할 수 있다.

 

 

 

 

 

참고자료1