[기계학습] 로지스틱 회귀 Logistic regression

 

로지스틱 회귀 (Logistic regression) 란?

쉽게 회귀가 아닌 분류 알고리즘이라고 생각하면 된다. 예를 들어 스팸메일인지/아닌지 병에 걸렸는지/아닌지 분류하는 것이다. sigmoid function을 사용하여 어떠한 사건이 발생할 가능성을 예측하고, 그 값은 항상 0에서 1사이 이다. 일반 회귀 분석은 종속변수로 올 수 있는 값이 제한적이지 않지만, 로지스틱 회귀분석은 종속변수로 올 수 있는 값이 제한적이다.

sigmoid function

sigmoid function은 어떤 x 가 입력값(독립변수)로 들어왔을 때 사건 발생 가능성으로, 이 함수의 값이 항상 0에서 1사이이다.

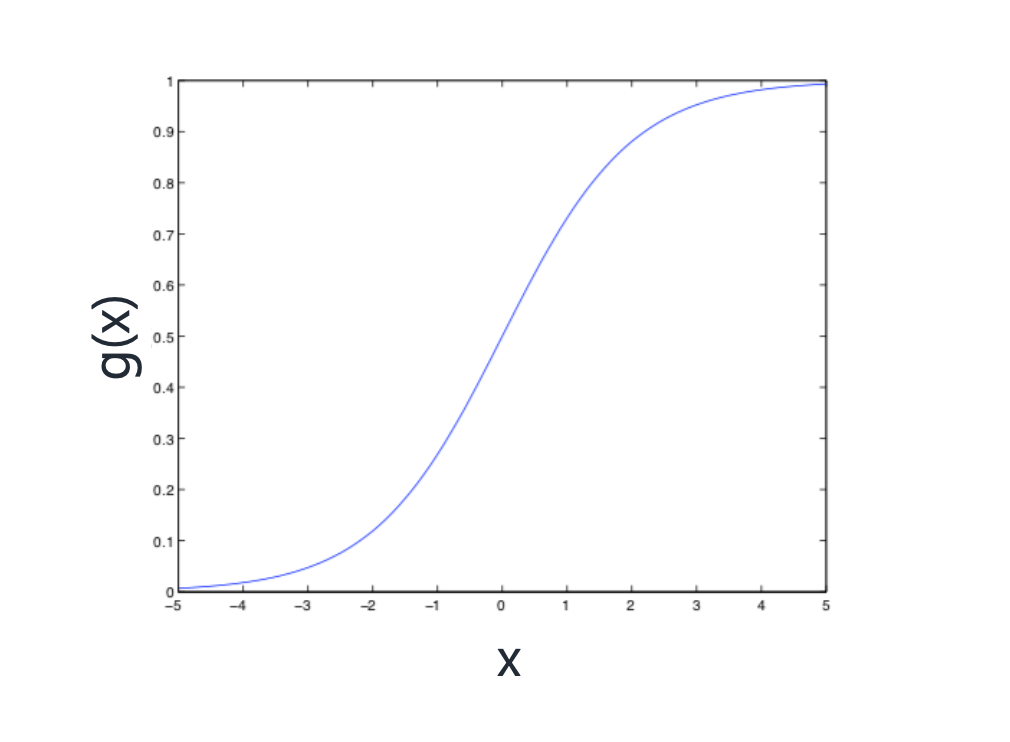
로지스틱회귀는 sigmoid function을 사용하기 때문에 값이 0에서 1로 제한되어 있는 것이다. sigmoid function은 위 그래프처럼 주로 s커브의 형태를 한다.

sigmoid function은 종속변수가 제한적이기 때문에 분류에 사용하기 좋다. 예를 들어 값이 0.5 이상이면 스팸메일에 분류하고, 0.5미만이면 일반메일에 분류하는 것처럼 말이다.

 

Likelihood

Logistic Regression의 likelihood를 생각해보자

Likelihood는 주어진 데이터가 주어진 모델 또는 확률분포를 따를 확률이다. 함수의 파라미터(β)에 따라 값이 변한다. 

위 식은 x와 β가 관련이 있다. f(x)는 x와 β가 관련이 있을때, 실제 스팸 메일이 종속변수가 1로(스팸메일)로 분류될 확률을 나타낸다. 즉 스팸메일이 올바르게 분류될 확률을 나타낸다는 것이다.  (여기서 학습 데이터들은 모두 독립적이라는 것을 알아야한다.)

Likelihood는 결국 Logistic Regression이 올바르게 작동하는 확률로 이해할 수 있으므로, Likelihood의 값이 커야 맞게 분류될 확률이 크다. 따라서 우리는 Likelihood 를 최대화 해줄 수 있는 파라미터 β를 찾아야한다

그럼 어떻게 likelihood 를 최대화해주는 β를 찾을 수 있을까?

Gradient Ascent algorithm을 이용하면된다.

우리는 이전에 Gradien Descent algorithm 을 공부한적 있다. 어느 한 시점에서 기울기를 구해, 그 기울기가 작아지는 방향으로 움직임을 반복해서 점점 기울기를 줄여나가 결론적으로 global minimum을 찾는 알고리즘이었다. 논리는 동일하다. Gradient ascent 도 움직임을 반복하며 기울기를 크게하는 파라미터 β 값을 찾으면 된다. 단지 기울기가 작아지는 방향이 아닌, 커지는 방향으로 움직임을 반복하는게 다를 뿐이다