[알고리즘] 힙 정렬 (Heap Sort)
이진 힙 (Binary Heap)
: 힙 조건을 만족하는 완전 이진 트리
: 힙 조건 : 각 노드의 우선순위(priority)가 자식 노드의 우선 순위보다 높다
– 최대 힙(Maximum Heap): 가장 큰 값이 루트에 저장
– 최소 힙(minimum Heap): 가장 작은 값이 루트에 저장
ex) n개의 노드를 가진 힙
– 완전 이진 트리이므로, 힙의 높이가 log2n이며, 노드들을 빈 공간 없이 배열에 저장

힙의 노드 관계
힙에서 부모와 자식의 관계
– A[i]의 부모 = A[i/2] (단, i가 홀수이면 i/2에서 정수 부분만)
– A[i]의 왼쪽 자식 = A[2i]
– A[i]의 오른쪽 자식= A[2i+1]
힙 정렬 (Heap Sort)
루트에 가장 큰 수가 있는 최대 힙을 정렬한다고 하자
힙 루트에 가장 큰 수가 있으므로, 루트와 힙의 가장 마지막 노드를 교환한다. ( 가장 큰 수를 배열의 맨 뒤로 옮긴 것 )
제일 큰 수를 마지막 배열로 보냈으므로 힙 크기를 1개 줄인다.
루트에 새로 저장된 숫자로 인해 힙 조건이 위배되었을 수 ㅋ있으므로 이것을 해결하고 다시 루트노드를 맨 뒤로 보내는 과정을 반복한다
* 힙 조건이 위배되었을때 해결 방법 DownHeap() : 루트로부터 자식들 중에서 큰 값을 가진 자식과 비교하여 힙 속성이 만족될 때까지 숫자를 교환하며 이파리 방향으로 진행
밑에 있는 최대 힙을 정렬시킨다고 해보자

루트 노드에 있는 가장 큰 수 90과 맨 마지막 노드에 있는 숫자인 40을 바꾸어
제일 큰 수인 90을 배열 맨 뒤로 보낸다
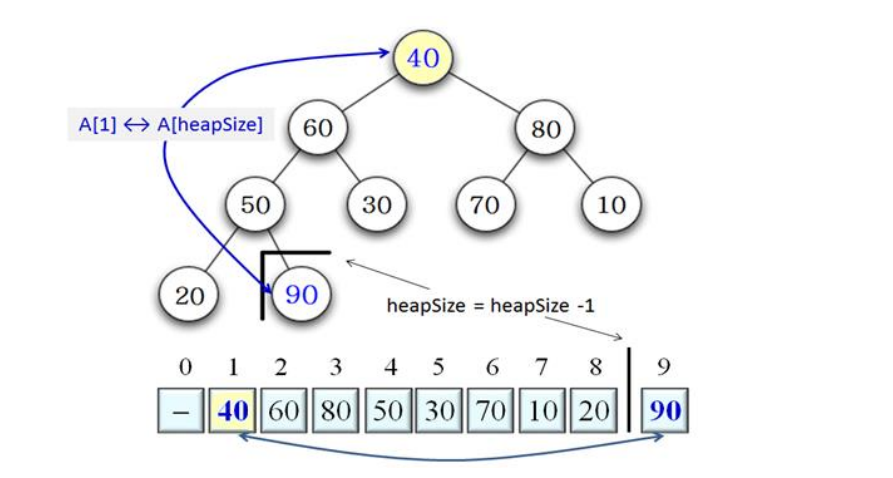
그리고 정렬이 끝난 90은 없는 노드라고 생각하고 힙을 1개 줄인다
맨 마지막에 있던 숫자인 40이 루트 노드에 가서 힙 조건에 위배된다 (부모 노드가 자식 노드보다 우선순위 높아야함)
그럼 이제 DownHeap()을 통해 자식 노드 중 더 큰 숫자 80과 루트 노드 40을 교체한다

또 부모노드인 40이 자식노드인 70보다 작으므로 두 개를 바꿔준다

이제 힙 조건에 위배되는게 없으므로 앞서 과정과 똑같이 루트노드에 있는 가장 큰 수 80을 가장 마지막 노드인 20과 바꾸어 배열 맨 뒤로 보낸다. 그리고 80은 정렬이 끝났으므로 힙 1개를 빼준다
그러면 20이 루트노드에 있으므로 힙 조건을 위배하기 때문에 자식 노드 중 큰 수인 70과 바꾸고, 또 40과 바꿔준다

이 과정을 계속해서 반복하면

정렬이 끝나게 된다
알고리즘
1. A의 숫자에 대해서 최대 힙을 만든다.
2. heapSize = n // 힙의 크기를 조절하는 변수
3. for i = 1 to n-1
4. A[1] ↔ A[heapSize] // 루트와 힙의 마지막 노드 교환
5. heapSize = heapSize -1 // 힙의 크기 1 감소
6. DownHeap() // 위배된 힙 조건을 만족시킨다.
7. return A우선 정렬할 최대 힙을 만들고,
(n-1)번 루트노드와 마지막 노드를 교체한다. 교체된 루트 노드는 이미 정렬이 완료된 숫자이므로 힙의 크기를 1 감소시킨다.
교체되는 과정에서 힙 조건에 위배되는 노드가 생기면 조건을 만족시킨다
시간복잡도
힙 만드는 데 O(n) 시간
for-루프는 (n-1)번 수행 – 루프 내부는 O(1) 시간
DownHeap은 O(logn) 시간
O(n) + (n-1) x O(logn) = O(nlogn)