[이취코] Ch09-3. 최단경로 / 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)
플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)
- 모든 지점에서 다른 모든 지점까지의 최단 경로를 구해야하는 경우에 사용할 수 있는 알고리즘
- 2차원 리스트에 '최단 거리' 정보를 이용한다
- 다이나믹 프로그래밍
플로이드 워셜 알고리즘은 단계마다 해당 노드를 거쳐가는 경우를 고려해 최단경로를 비교한다
예시를 들어 말하자면 A, 1, B 노드가 있고 A에서 B까지 가는 최단 경로를 구한다고 할 때
노드 1을 거쳐가는 경우(A-1-B)와 A에서 B로 가는(A-B) 경로를 비교해 더 작은 것을 최단 경로로 선택하는 것이다
점화식으로 표현하자면,

a에서 b까지 가는 경우의 최단 거리는 'a에서 바로 b로 가는 경우' 와 '노드 k를 거쳐 가는 경우' 중 작은 값이다
예시를 통해 구체적으로 보도록 하자

STEP0. 우선 초기테이블을 설정해준다
연결되어있는 간선은 단순히 그 값을 채워넣고, 연결되지 않은 간선은 무한이라는 값을 넣는다
* 무한은 임의의 큰 값을 의미한다
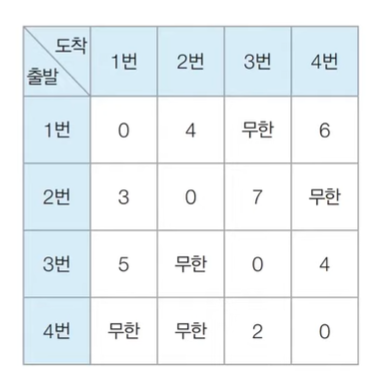
예를 들어 1번 노드에서 2번 노드까지 가는 간선의 값은 4이므로 표에 4을 넣어주고, 3번노드에서 1번노드를 가는 간선의 값은 5이므로 5을 넣어준다
STEP1. 1을 제외한 모든 노드가 1을 거쳐 가는 경우를 고려한다
(1을 제외한 노드 중 순서대로 두 노드를 선택한 경우를 고려하는 것 이므로 3P2 경우의 수를 고려해주면 된다)
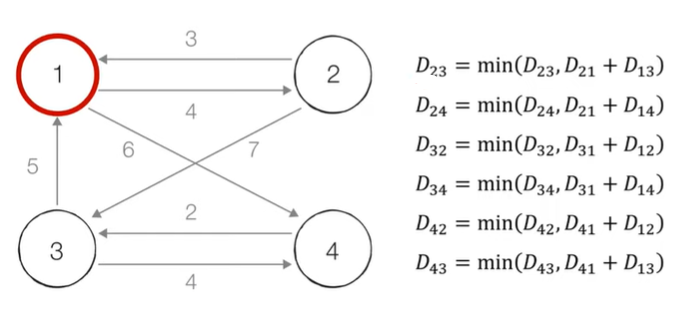
이 6가지 경우만 계산하여 값을 갱신하면 된다
하나를 예로 들자면 D23은 노드2에서 노드3으로 연결되어 있는 값과 1을 거쳐서 (노드2-노드1-노드3) 가는 경우를 비교해 더 작은 값을 골라 갱신하면 된다
테이블을 갱신하면
| (행) 출발 노드 (열) 도착 노드 |
1 | 2 | 3 | 4 |
| 1 | 0 | 4 | 무한 | 6 |
| 2 | 3 | 0 | 7 | 9 |
| 3 | 5 | 9 | 0 | 4 |
| 4 | 무한 | 무한 | 2 | 0 |
파란색 글자 부분이 값을 비교한 6가지 경우이고 예를 들어 하나를 보자면
D24는 원래 무한의 값을 가졌는데 1을 거쳐 D21+D14=3+6=9 로 갱신되었다
STEP2. 2을 제외한 모든 노드가 2을 거쳐 가는 경우를 고려한다

STEP1과 마찬가지로 여섯가지 경우를 고려해주면 된다 (3P2)
| (행) 출발 노드 (열) 도착 노드 |
1 | 2 | 3 | 4 |
| 1 | 0 | 4 | 11 | 6 |
| 2 | 3 | 0 | 7 | 9 |
| 3 | 5 | 9 | 0 | 4 |
| 4 | 무한 | 무한 | 2 | 0 |
D13이 원래 무한 값이었는데 2를 거쳐서 D12+D23=4+7=11 로 갱신되었다
STEP3. 3을 제외한 모든 노드가 3을 거쳐 가는 경우를 고려한다
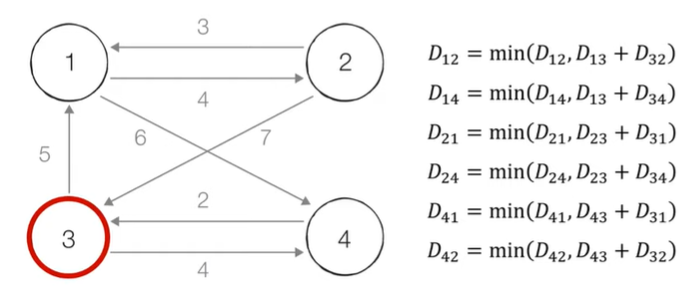
3도 마찬가지로 위와 같은 방법을 반복하면
| (행) 출발 노드 (열) 도착 노드 |
1 | 2 | 3 | 4 |
| 1 | 0 | 4 | 11 | 6 |
| 2 | 3 | 0 | 7 | 9 |
| 3 | 5 | 9 | 0 | 4 |
| 4 | 7 | 11 | 2 | 0 |
테이블이 이렇게 초기화된다
마지막으로
STEP4. 4을 제외한 모든 노드가 4을 거쳐 가는 경우를 고려한다
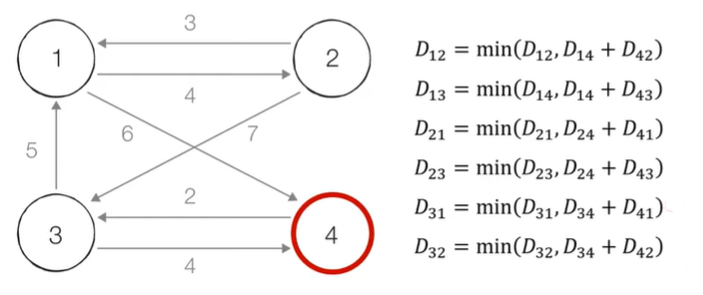
마찬가지로 6가지 경우를 계산하면
| (행) 출발 노드 (열) 도착 노드 |
1 | 2 | 3 | 4 |
| 1 | 0 | 4 | 8 | 6 |
| 2 | 3 | 0 | 7 | 9 |
| 3 | 5 | 9 | 0 | 4 |
| 4 | 7 | 11 | 2 | 0 |
테이블이 이렇게 갱신이되고, 이것이 최단경로 테이블이 된다
코드로 구현하자면
#include <iostream>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
using namespace std;
// 노드의 개수(N), 간선의 개수(M)
// 노드의 개수는 최대 500개라고 가정
int n, m;
// 2차원 배열(그래프 표현)를 만들기
int graph[501][501];
int main(void) {
cin >> n >> m;
// 최단 거리 테이블을 모두 무한으로 초기화
for (int i = 0; i < 501; i++) {
fill(graph[i], graph[i] + 501, INF);
}
// 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
if (a == b) graph[a][b] = 0;
}
}
// 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for (int i = 0; i < m; i++) {
// A에서 B로 가는 비용은 C라고 설정
int a, b, c;
cin >> a >> b >> c;
graph[a][b] = c;
}
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for (int k = 1; k <= n; k++) {
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// 수행된 결과를 출력
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
// 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if (graph[a][b] == INF) {
cout << "INFINITY" << ' ';
}
// 도달할 수 있는 경우 거리를 출력
else {
cout << graph[a][b] << ' ';
}
}
cout << '\n';
}
}플로이드 워셜 알고리즘의 시간 복잡도는
노드의 개수가 N개일 때 알고리즘 상으로 N번의 단계를 수행하며, 단계마다 O(N^2) (=P연산) 연산을 통하므로
총 시간 복잡도는 O(N^3)이다 (삼중 반복문으로도 판단이 가능하다)