[기계학습] 정규화 : Ridge regression / Lasso regression
우리가 데이터 분석을 할 때, underfitting 과 overfitting 의 경우가 있다.

underfitting 의 경우 함수는 단순하지만 몇몇 데이터가 커버되지 않는다는 단점이 있고,
overfitting 의 경우 데이터는 잘 커버되지만 함수가 너무 복잡해진다는 단점이 있다. 또한 이미 현재의 데이터에 최적화되어있기 때문에 새로운 데이터가 들어왔을 때 잘 동작하지 않을 것이라는 단점이 있다.
따라서 underfitting과 overfitting의 중간지점을 찾아야하는데, 어떻게 해야할까?
과적합 문제를 해결하기 위해 우리는 정규화 방법을 사용한다
정규화를 하기 전에 bias 와 variance를 먼저 이해할 필요가 없다
Bias 란, 평균 예측값과 실제 값 사이 차이를 뜻하고
Variance 란, 각각 데이터 예측 값의 다양성을 뜻한다
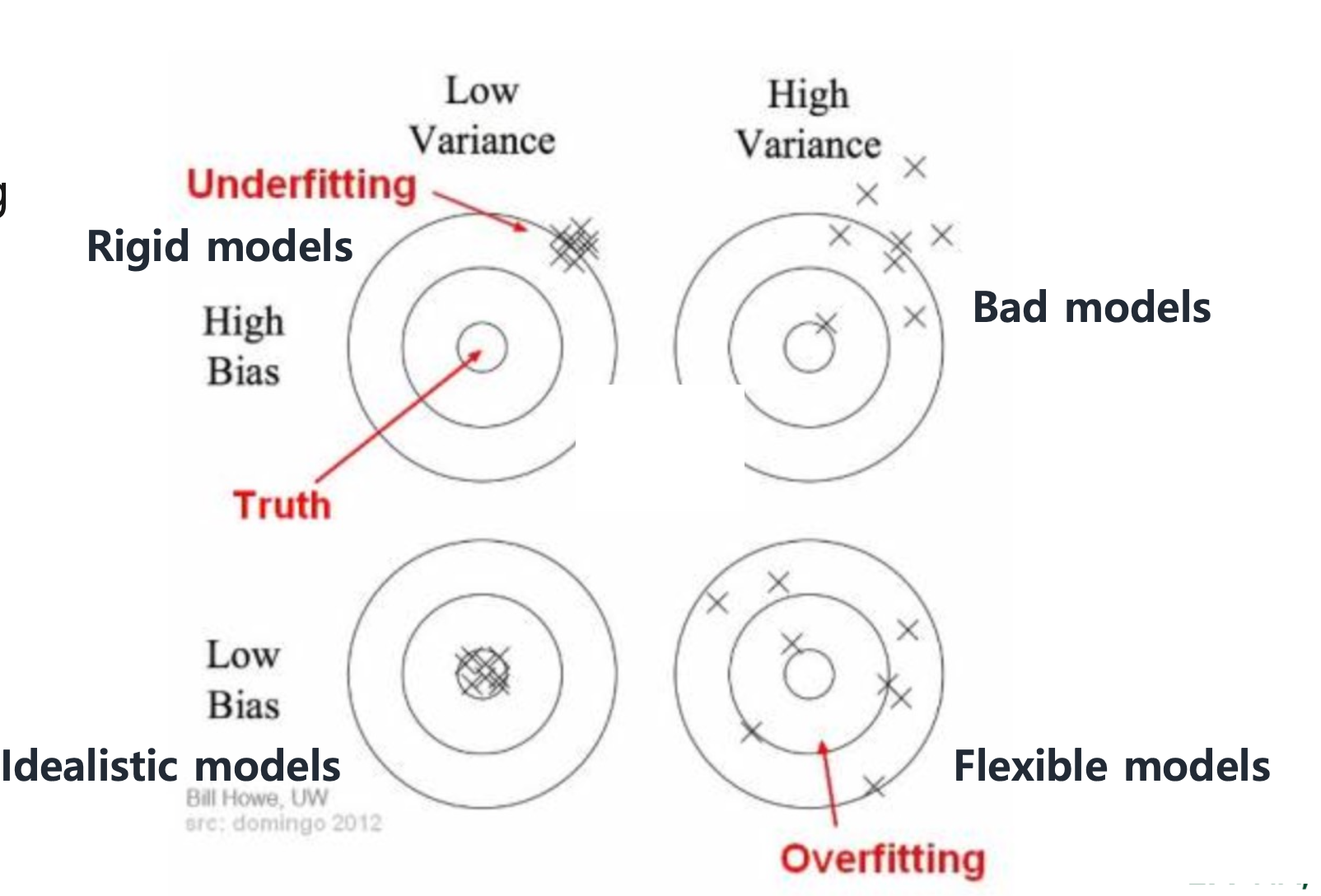
이 그림에서 보는 것과 같이 bias가 작다는 것은 과녁에 잘 편향되어져있다는 뜻이다. 그리고 variance가 작다는 것은 얼마나 흩어져있냐를 말한다. 그래서 둘을 다 줄이는 것이 좋은데, 사실 둘은 trade-off 관계가 있다.

Bias 와 Variance 를 균형잡을 수 있는 방법은 위 그래프와 같이 총 에러의 최소값을 구하는 것이다
또한 더 많은 파라미터를 더하면 underfitting 의 문제는 해결 할 수 있다.
하지만 그럼 overfitting 은 어떻게 할까? model 의 complexity 를 감소시켜야한다.
model complexity를 줄이기 위해서는 정규화를 이용해야 되는데,
이 정규화는 크게 Ridge 와 Lasso Regularization 으로 나뉜다
Ridge regression
Ridge regression은 L2 normalization 를 이용한다
L2 normalization 은 각각의 값을 제곱해서 더한 총합이다
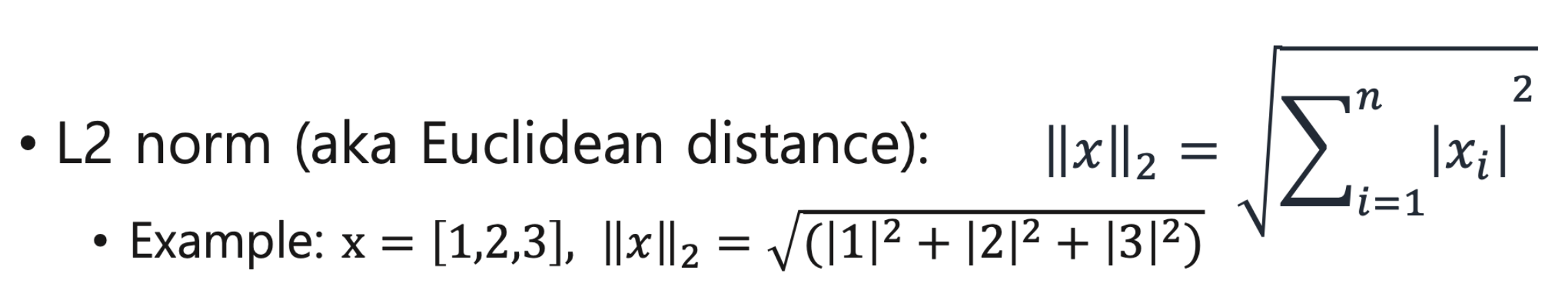
Ridge regression 은 L2 normalization 을 이용해서 어떤 범위로 제약을 주고, 패털티 값을 더해서 파라미터를 줄이는 것이다
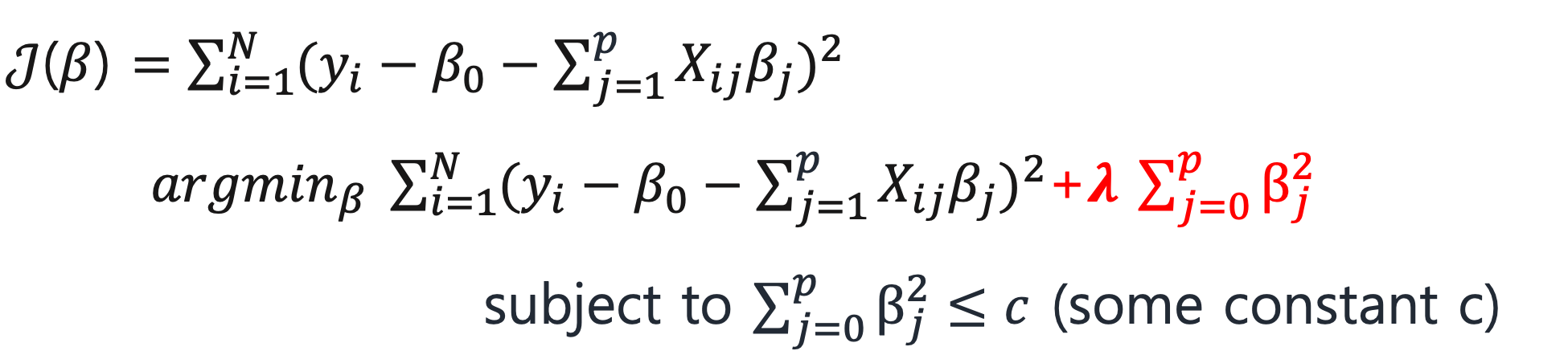
여기서 빨간색에 해당하는 부분이 더해지는 패널티인데,
β가 클수록 패널티가 커지고, β가 작을수록 패널티도 작아진다
Ridge Regression 에 적용되는 제약조건이 제곱의 형태이기 때문에
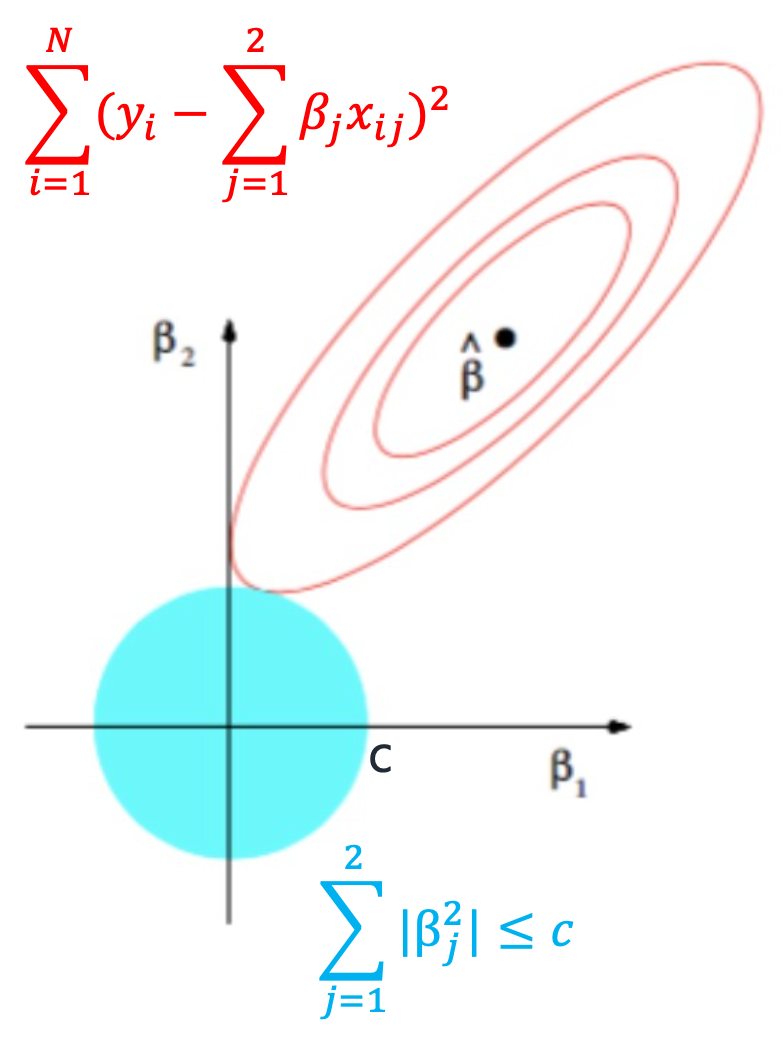
위 사진처럼 제약조건이 원의 형태로 그려진다
가장 가운데에 있는 β가 제약조건 없는 경우 에러 최소로, 과적합한(overfitting) 상태라고 보면 된다
그 중심에서 점점 타원형태로 멀어질수록 overfitting 이 완화되어 에러가 커진다고 생각하면 된다그리고 타원과 제약조건이 만나는 지점이 overfitting 과 underfitting의 중간지점이다
Lasso regression
Lasso regression 은 L1 normalization 을 이용하는 것이다.

L1 normalization 는 각 절대값을 다 합한 값이다
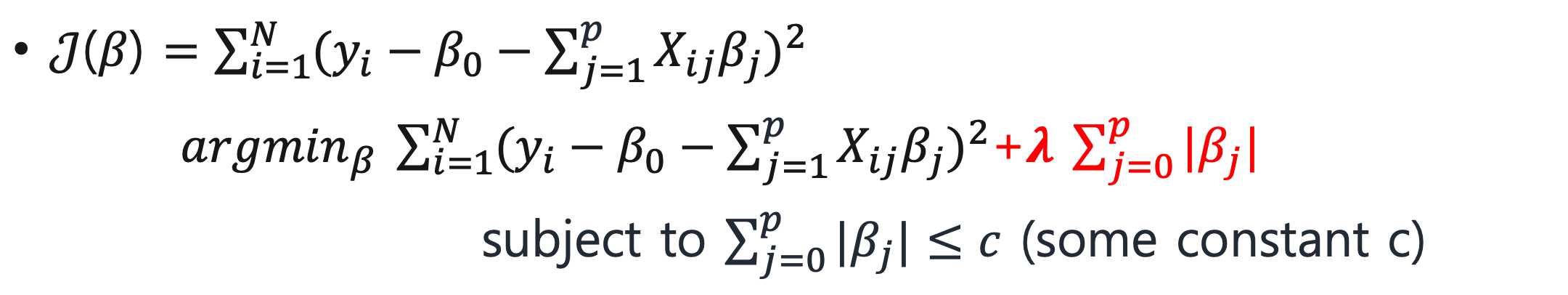
마찬가지로 패널티를 더해 오류를 감소하는 방법인데, 제약조건이 다르다
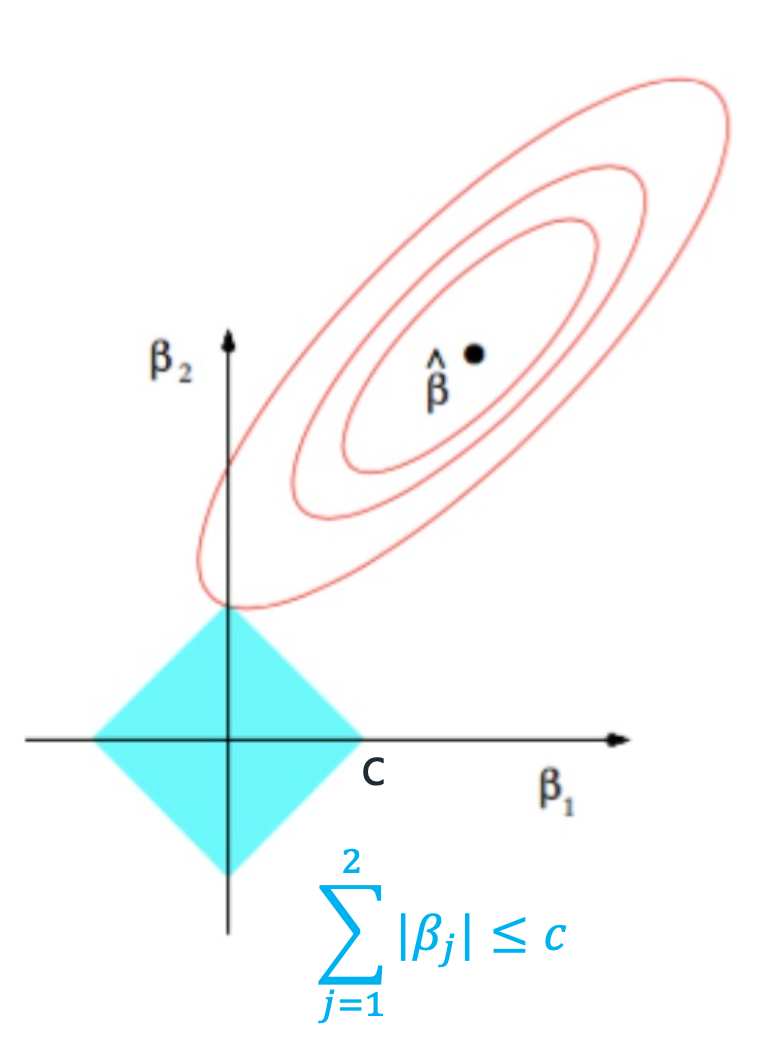
lasso는 제약조건이 절대값이기 때문에 위 그래프처럼 마름모의 형태가 나오고 뾰족한 부분이 β가 0이 되는 지점이다.
Lasso regression 의 특징은 Feature selection 을 사용할 수 있다는것인데,
feature selection이란 0이 되는 베타 값을 아예 무시할 수 있다는 것이다
Ridge regression은 파라미터가 0에 가까워지긴 하지만 0이 될수는 없어 feature selection 을 사용할 수 없다. 그래서 이게 Ridge regression 과 lasso regression 의 차이점이기도 하다
따라서 만약 고차원인 feature space가 있다고 할 때, 어느 것이 더 유리한가?한다면 Lasso regression은 feature selection 을 쓸 수 있기 때문에 Ridge regression 보다 Lasso regression 이 더 유리하다
또한, 앞에서 살펴봤던 Ridge 와 Lasso 패널티에 모두 있는 람다에 따라 패널티에 값이 바뀐다. 람다의 값이 클수록 패널티가 더 커진다
따라서, 람다가 클수록 변수는 적어지고 모델은 간단해지지만 underfitting에 가까워지고
람다가 작을수록 변수는 많아지고 모델은 복잡해져 overfitting의 위험이 증가한다