[기계학습] 국소회귀 Locally weighted linear regression
선형회귀를 사용해서 과연 데이터들을 언제나 올바르게 나타낼 수 있을까? 를 생각해보면 그렇지않다.
아래와 같은 경우를 보자

왼쪽 그래프는 선형 회귀를 사용한 것이지만 함수가 커버하지 못하는 데이터들이 많다.
오히려 왼쪽 그래프보다 오른쪽 그래프가 현재 가지고있는 데이터를 더 잘 나타낸다고 할 수 있다
오른쪽 그래프처럼 변수를 추가함으로써 데이터를 더 잘 커버할 수 있다.
하지만, 데이터가 더 많아지면 어떤 경우가 생길까?

왼쪽 그래프는 복잡하지 않지만 함수가 커버하지 못하는 데이터들이 많다. 우리는 이것을 underfitting 이라고 한다.
오른쪽 그래프는 모든 데이터를 잘 커버하고 있지만 함수가 너무나도 복잡하다. 우리는 이것을 overfitting 이라고 한다.
그럼 그렇게 복잡하지 않으면서 데이터를 어느정도 잘 커버할 수 있는 underfitting과 overfitting의 중간지점을 찾아야하는데, 이것을 우리는 국소회귀 (Locally Weighted Linear Regression)을 통해서 찾을 수 있다.
머신러닝 알고리즘은 두 가지 타입의 알고리즘으로 나뉜다
파라메트릭 학습 알고리즘(Parametric Learning Algorthm)은 주어진 데이터를 가지고 최적의 파라메타(모수)를 찾아 정하는 방법이다. 파라미터의 개수가 고정적이고, input의 사이즈의 따라 개수가 바뀔 수 없다. 선형회귀분석이 여기에 해당한다
비파라메트릭 학습 알고리즘(Non-Parametric Learning Algorthm)은 주어지는 데이터의 양에 따라서 파라메타 값을 누적해가면서 파라메타를 찾고 정의하는 방법이다. 파라미터의 개수가 정해져있지않아 학습데이터량에 따라 파라미터가 증가하거나 감소할 수 있다.
Locally Weighted Linear Regression는 비파라메트릭 방법중 하나로 그 컨셉은 이름에 나와있는 것처럼 로컬에 중심해서 회귀선을 만들고 추정하는 방법이다.
타겟데이터와 가까운 점들만 학습데이터로 이용하고, 타겟 데이터와 먼 점들은 학습데이터에서 제외한다고 생각하면 된다.
수식을 살펴보자

이전 선형회귀(Linear Regression Model)과는 다르게 w라는 계수가 있다

w는 0과 1사이로 얼마나 가중치를 둘 것인지를 결정한다.
만약 x(i)-x가 작다면, w는 1에 가까워질것이고, x(i)-x가 크다면 w는 0에 가까워질 것이다
x(i)-x가 작다는 것은 x(target variable)과 x(i)의 차이가 크지않다는것. 즉 가깝다는 뜻이므로 가중치가 1에 가깝다. x와 가까운 점들이 큰 영향을 미치기 때문에 이 점들을 우리는 고려해야한다.
가중치 w가 0에 가깝다면 x에서 먼 점들이기 때문에 학습데이터에서 무시가 가능하다.

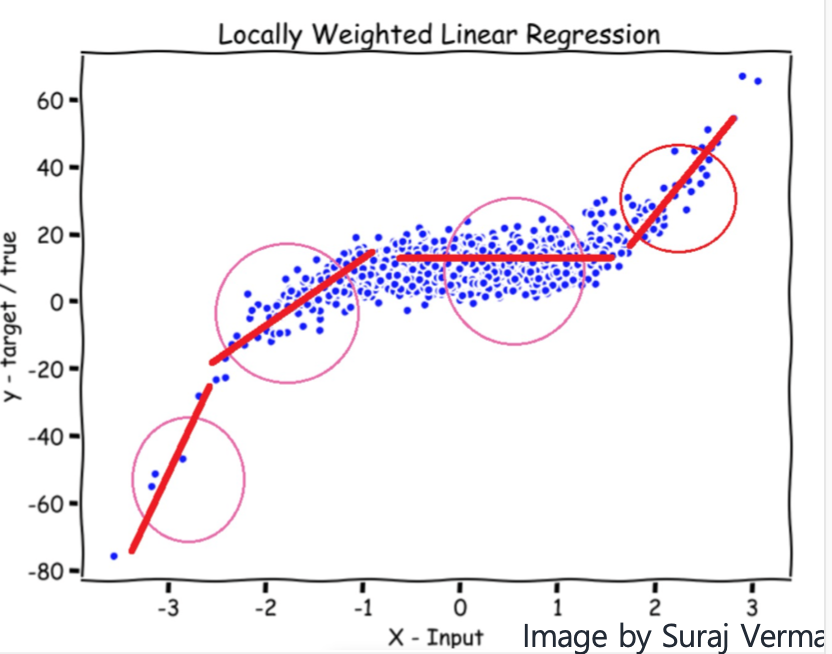
이처럼 Locally Weighted Linear regression은 좁은 범위의 데이터를 한정해서 비선형문제를 선형으로 취급하는 방법이다.
이걸 bandwidth 로도 표현할 수 있는데, 위 수식에서

분모가 bandwidth에 해당한다.

색칠된 bandwidth 는 x로부터 얼마나 가까운 점들만 고려할건지 결정한다
따라서 Local Weighted Linear Regression 은 가까운 데이터들만 고려했을떄는 선형으로 보이지만, 전체적으로 봤을때는 결국 non linear 형태가 된다
참고자료
https://nanunzoey.tistory.com/entry/국소-회귀Locally-Weighted-Regression란